IMPROVEMENT OF YIELD CURVE ARBITRAGE TRADING MODEL ON RUSSIAN GOVERNMENT BOND MARKET
Proskuryakov Ivan M.
Abstract
This article is motivated by a necessity for fixed income market participants to extract profit from operations with securities avoiding market risk, that is possible by usage of our proposed arbitrage trading model. In the article we provide the theoretical fundament of arbitrage trading and its specifics in realizing pure arbitrage and relative value arbitrage. The mechanism of yield curve arbitrage is disclosed in the article, as well as its types (steepener, flattener and butterfly trades) are described. The performance of yield curve arbitrage trading models for 7 pairs of Russian OFZ-bonds with different maturities is evaluated. The main method of investigation was back testing of trading models on real historic data of zero-coupon OFZ yield curve. We developed the author’s optimal trading model with two new parameters: simple moving average of the yield spread and size of deviation from moving average which is the trigger for opening the position. The result of back testing proved the superiority of our model in comparison with elder (cumulative) model. We developed the author’s optimal trading model with inclusion of new parameters – simple moving average of yield spread and degree of deviation from mean, which is the trigger for opening the position. We executed the optimization of parameters of authors trading models based on the maximization of Sharpe ratio. Back testing proved the superiority of our model over the elder (cumulative) model. Analysis showed that the most efficient is the arbitrage trading with instruments which difference of maturity does not exceed one year. Comparison of spot yield spread with simple moving average of spread for last several months (from 5 to 13) for detecting arbitrage opportunities and setting the minimum deviation from mean as the trigger level affords to improve the trading model as it starts to generate higher return without increasing the volatility as the back testing reflects. This investigation is of interest of hedge funds making fixed income arbitrage and other professionals in portfolio management.
Keywords: arbitrage, fixed income, OFZ, yield curve, trading model, trading strategy, algorithmic trading
СОВЕРШЕНСТВОВАНИЕ ТОРГОВОЙ МОДЕЛИ АРБИТРАЖА КРИВОЙ ДОХОДНОСТИ НА РЫНКЕ ОФЗ
Проскуряков Иван Михайлович
Аннотация
Данное исследование мотивировано необходимостью для участников рынка долговых инструментов систематически извлекать прибыль из операций с ценными бумагами, избегая рыночного риска, что возможно с помощью предлагаемой нами арбитражной торговой модели. В статье приводятся теоретические основы арбитражной торговли и ее специфики при реализации чистого арбитража и арбитража относительной стоимости, раскрывается механизм арбитража кривой доходности и описываются его разновидности – сделки стипенер, флэтенер и бабочка. Оценена эффективность торговых моделей арбитража кривой доходности по семи парам облигаций-ОФЗ разной срочности. Основным методом исследования послужило обратное тестирование торговых моделей на реальных исторических значениях бескупонной кривой доходности российских ОФЗ. Создана авторская оптимальная торговая модель с включением в нее новых параметров – простое скользящее среднее спреда доходности и величина отклонения от среднего, служащего триггером для открытия позиций. Проводилась оптимизация параметров авторской торговой модели с точки зрения максимизации коэффициента Шарпа. Результат обратного тестирования показал превосходство нашей модели над более старой (кумулятивной) моделью. Анализ показал, что наибольшую эффективность дает арбитражная торговля инструментами с разницей в сроке погашения не более 1 года. Сравнение спотового спреда доходности со скользящим средним периода за несколько месяцев (от 5 до 13) для выявления арбитражных возможностей и установка минимальной величины отклонения от среднего, служащего триггером для открытия позиций, позволяет усовершенствовать торговую модель, так как она начинает в таком случае приносить большую доходность без увеличения волатильности, как было показано при тестировании на исторических данных. Данное исследование может представлять интерес для хедж-фондов, занимающихся арбитражем на рынке долговых инструментов и других профессионалов в области портфельного менеджмента.
Ключевые слова: арбитраж, рынок облигаций, ОФЗ, кривая доходности, торговая модель, торговая стратегия, алгоритмический трейдинг
Торговля долговыми инструментами и их деривативами является прибыльным бизнесом для инвестиционных банков мира. Помимо предоставления рыночной ликвидности за счет маркет-мэйкерства инвестиционные банки также уделяют значительную часть собственного капитала на торговлю широким спектром долговых инструментов, таких как казначейские ценные бумаги (от 3-месячных векселей до 30-летних облигаций), корпоративные облигации, ипотечные ценные бумаги и т.д. Помимо инвестиционных банков, хедж-фонды и специализированные фонды облигаций также активно ищут торговые возможности на рынке долговых инструментов и их деривативов.
Стратегии, которыми участники рынка пользуются, разнятся, начиная от чистого арбитража, заканчивая сложными сделками, основанных на прогнозах технического анализа и ожиданиях относительно срочной структуры процентных ставок и кредитных рисков. Стратегии кривой доходности, по сути, подразумевают сделки на изменения в срочной структуре процентных ставок. Такие стратегии могут быть широко классифицированы как направленные и основанные на относительной стоимости. Направленные стратегии, как и подразумевает название, предполагают сделки на изменение процентных ставок в определенном направлении. Стратегии относительной стоимости, напротив, основываются на представлении, что безусловная кривая доходности имеет восходящий наклон, и, что текущая кривая доходности возвратится к среднему (к безусловной кривой доходности).
Существует два типа арбитража на финансовых рынках: арбитраж относительной стоимости и чистый арбитраж. Последний в теории предполагает извлечение прибыли без риска. Когда два взаимозаменяемых актива торгуются по разным ценам, то имеет место возможность чистого арбитража. В контексте арбитража на рынке долговых инструментов и их деривативов чистый арбитраж реализуется при отклонениях вмененной ставки РЕПО фьючерса на единичную облигацию от фактической ставки РЕПО базовой облигации, при отклонениях рынка опционов на процентные ставки от пут-колл паритета [10, c. 104-105] и при отклонениях от покрытого процентного паритета [9].
Чистый арбитраж встречается редко, в то же время арбитраж относительной стоимости открывает множество привлекательных возможностей для арбитражера, который может принять на себя некоторый риск. Идея арбитража относительной стоимости в том, что арбитражер находит два актива, которые имеют историческую взаимосвязь, открывает противоположные позиции тогда, когда данная взаимосвязь нарушается, и фиксирует прибыль, когда взаимосвязь приходит в нормальное состояние.
Арбитраж кривой доходности — это разновидность арбитража относительной стоимости. Парой активов в таком случае являются две безрисковых (государственных) облигации с разными сроками погашения.
Кривая доходности – это графическая репрезентация взаимосвязи между доходностями облигаций одного кредитного качества с разными сроками до погашения [8, c. 173]. Временная структура процентных ставок – одно из определений кривой доходности. Уровень и наклон кривой доходности может изменяться, как функция политики Центрального Банка страны, кредитоспособности эмитирующего государства, баланса спроса и предложения, новых выпусков, а также от условий, относящихся к стадии бизнес-цикла, которую проходит государство.
Существует традиционное представление на рынке долговых инструментов, что кривая доходности склонна возвращаться к среднему. Имеются исследования, подтверждающие данное представление [1, 2]. Арбитраж кривой доходности может быть основан на концепции возврата к среднему, которая предполагает, что позиция открывается на основе прогноза, что спред доходности возвратится к своему историческому среднему. Таким образом, отклонение от среднего интерпретируется как неправильная оценка рынком. Арбитраж кривой доходности – это торговая стратегия, при которой арбитражер открывает длинные и короткие позиции по разным точкам кривой доходности государственных облигаций определенной страны, чтобы извлекать прибыль из временной неправильной относительной оценки между данными разными точками.
Арбитраж кривой доходности может принимать форму сделок стипенер, флэтенер и бабочка. Если арбитражер ожидает, что спред доходности (к примеру, между длинным и коротким концом кривой) расширится, он вступает в сделку стипенер, открывая длинную позицию по краткосрочной облигации и короткую позицию по долгосрочной облигации. Таким образом, стипенер – это ставка на увеличение крутизны кривой доходности. Если арбитражер ожидает сужения спреда доходности, он вступает в сделку флэтенер, открывая противоположные стипенеру позиции, делая ставку на снижение крутизны кривой доходности.
Бабочка – это сделка на основе ожидаемых изменений кривизны кривой доходности. Бабочка предполагает открытие позиций в трех точках кривой доходности, которые составляют комбинацию штанги и пули [7]. Штанга – это однонаправленные позиции по двум разным точкам кривой доходности, а пуля в данном случае – это позиция в одной точке кривой доходности между точками штанги и направленная противоположно штанге. Риск и доходность бабочки, как разновидности арбитража кривой доходности были исследованы Дюартом с соавторами [4] на месячных данных процентных свопов, основанных на libor за период с 1988 по 2004 гг. Их стратегия была основана на двухфакторной модели срочной структуры процентных ставок, которая была подогнана так, чтобы соответствовать наблюдаемым ставкам 1-летних и 10-летних свопов. Если ставка 2-, 3-, 5- или 7-летнего свопа отклонялась от модельной ставки более чем на 10 базисных пунктов, открывалась позиция на возврат к модельному значению, захеджированная противоположными позициями по 1-летнему и 10-летнему свопам. Результаты исследования показали, что данная стратегия генерирует значительную положительную альфу.
Под торговой моделью мы понимаем алгоритмизованную торговую стратегию, т.е. стратегию, сформулированную в таком виде, в каком она может генерировать автоматические торговые решения, и, следовательно, может быть протестирована на исторических данных.
Арбитраж кривой доходности может предполагать извлечение прибыли из отклонений угла наклона и кривизны кривой доходности от справедливых значений. В данной статье мы будем анализировать торговые модели, основанные на игре на изменениях угла наклона кривой доходности. Каждая торговая модель подразумевает открытие позиций стипенер или флэтенер в соответствующих рыночных условиях, используя два инструмента – бескупонные облигации с разным сроком погашения.
Чуа, Кох и Рамасвэми [3] исследовали эффективность торговых стратегий кривой доходности, основанных на возврате к среднему, на данных фондового рынка США с 1973 по 2000 гг. Стратегия стипенер/флэтенер (стратегия возврата к среднему спреда доходности) и стратегия бабочка показали значительное превышение доходности бенчмарков после поправки на риск.
Стратегия стипенер/флэтенер в первой версии подразумевала открытие арбитражных позиций на сужение (расширение) спреда доходности при превышении (недоборе) спреда 1-месячных форвардных ставок относительно соответствующего безусловного спреда. Безусловный спред принимался за справедливый уровень и рассчитывался как среднее значение спреда за все предшествующие месяцы. База для расчета безусловного спреда увеличивалась кумулятивно (нарастающим итогом), поэтому мы назовем стратегии рассматриваемого исследования кумулятивными.
Открытые позиции закрывались через месяц, после чего в зависимости от относительных значений спреда 1-месячных форвардных ставок и безусловного спреда открывались новые позиции. И нашу и кумулятивную модель мы тестировали таким же образом, учитывая срок удержания позиции равным одному месяцу.
Предлагаемый нами подход отличается от кумулятивного тем, что безусловный спред рассчитывается в виде n-месячного простого скользящего среднего рыночного спреда доходности, что позволяет рассматривать справедливое значение в динамике и более гибко подстраиваться под изменения рынка.
Второе отличие нашей торговой модели состоит в том, что сравнивается с безусловным спредом не спред форвардных ставок, а простой текущий спред спотовых ставок.
Третье отличие нашего подхода в том, что выявляются и, где необходимо, задаются оптимальные уровни триггера на открытие позиций, т.е. величины отклонения спотового спреда от безусловного спреда, которые дают сигнал об открытии позиции на возврат спреда к среднему. Если уровни триггеров не достигнуты, портфель остается вне рынка и зарабатывается нулевая избыточная доходность.
Будем далее называть наш подход оптимальным и торговые модели данного подхода – оптимальными.
Далее мы сравним эффективность обоих подходов (кумулятивного и оптимального) при обратном тестировании на данных российского рынка государственных облигаций.
Мы проанализировали 7 пар облигаций (15лет-0.5лет, 1лет-0.5лет, 2лет-1лет, 3лет-2лет, 5лет-3лет, 10лет-5лет и 15лет-10лет) на которых производился арбитраж кривой доходности на основе принципа возврата спреда доходности облигаций к историческому среднему. Исходные данные представляют собой ставки бескупонной доходности ОФЗ по всему спектру кривой доходности за период с апреля 2010 г по декабрь 2017 г, полученные из терминала Bloomberg. На основе их были рассчитаны цены гипотетических бескупонных государственных облигаций.
Поскольку дюрация бескупонных облигаций равна их сроку до погашения, коэффициенты хеджирования рассчитывались так, чтобы объем позиции (в лотах) по более краткосрочной облигации был больше объема позиции по долгосрочной облигации во столько раз, во сколько раз больше срок до погашения долгосрочной облигации относительно краткосрочной.
Все позиции в нашей модели финансируются с помощью соглашений РЕПО. Делается допущение о нулевых дисконтах РЕПО, чтобы не было потребности в собственном капитале. Длинная позиция открывается с помощью прямого РЕПО, а короткая - с помощью обратного РЕПО. Для учета денежных потоков, связанных с РЕПО, мы используем NFEA repo 1-month index, полученный из терминала Bloomberg. Данный индекс покрывает период с 01.2013 по 12.2017. Ввиду отсутствия данных под одномесячному РЕПО с 04.2010 по 12.2012, данный пробел мы заполнили данными 1-месячной Mosprime rate, полученными из терминала Bloomberg.
Для тестирования кумулятивных торговых моделей были рассчитаны одномесячные форвардные ставки для каждого срока погашения. Поскольку срок до погашения t облигации через один месяц становится равным t-1, то чтобы получить доходности для облигаций на момент закрытия позиций мы применили метод линейной интерполяции процентных ставок [5].
Для выявления оптимальных параметров наших торговых моделей мы тестировали различные периоды простого скользящего среднего (Simple moving average – SMA) спотового спреда соответствующей пары облигаций, а также уровни триггеров для открытия позиций. Итоговое предпочтение отдавалось той комбинации параметров, которая отражалась в максимальном коэффициенте Шарпа (отношении доходности к стандартному отклонению доходности) торговой модели.
Для расчета коэффициента Шарпа мы не учитывали безрисковую доходность. Размер условного собственного капитала, который был нужен для расчета доходностей моделей в %%, задавался таким, чтобы аннуализированная волатильность (стандартное отклонение) была равной 30%, или 8,66% в месячном выражении. Чтобы получить аннуализированный коэффициент Шарпа, месячный коэффициент Шарпа умножался на корень из 12. Такой порядок обусловлен тем, что делается допущение, что месячные доходности имеют незначительную автокорреляцию [6].
В таблицах 1 и 2 приведены показатели эффективности кумулятивных и оптимальных торговых моделей соответственно. В пяти парах облигаций из семи рассматриваемых пар оптимальные торговые модели показали более высокий коэффициент Шарпа, что говорит об их более высокой доходности при равной волатильности. Коэффициент средний выигрыш/проигрыш также выше у оптимальных торговых моделей по пяти из семи пар облигаций, что также говорит в пользу большей эффективности оптимального подхода. Зеленым в таблице показателей оптимальных моделей отмечено превышение показателя над соответствующим показателем кумулятивной модели.
Таблица 1. Показатели эффективности кумулятивных торговых моделей.
|
Пара |
15-0,5 |
1-0,5 |
2-1 |
3-2 |
5-3 |
10-5 |
15-10 |
|
Коэффициент Шарпа |
-1,659 |
0,279 |
0,01 |
0,282 |
0,191 |
0,13 |
-0,134 |
|
Месячная волатильность, % |
8,66 |
8,66 |
8,66 |
8,66 |
8,66 |
8,66 |
8,66 |
|
Средняя доходность/месяц, % |
-4,15 |
0,70 |
0,03 |
0,71 |
0,48 |
0,32 |
-0,34 |
|
Кол-во F |
13 |
32 |
27 |
23 |
18 |
29 |
10 |
|
Кол-во S |
66 |
47 |
52 |
56 |
61 |
50 |
69 |
|
Кол-во 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Кол-во + |
15 |
35 |
42 |
46 |
44 |
41 |
42 |
|
Кол-во - |
56 |
44 |
37 |
33 |
35 |
38 |
37 |
|
Средний выигрыш, % |
5,99 |
7,32 |
5,33 |
6,21 |
5,48 |
5,73 |
5,50 |
|
Средний проигрыш, % |
7,46 |
4,58 |
6,00 |
6,98 |
5,82 |
5,51 |
6,95 |
|
Средний выигрыш/проигрыш |
0,803 |
1,601 |
0,889 |
0,891 |
0,943 |
1,04 |
0,79 |
|
Асимметрия |
-2,335 |
1,67 |
1,362 |
-0,825 |
-2,204 |
-2,065 |
-1,243 |
|
Эксцесс |
11,429 |
6,223 |
8,815 |
2,17 |
14,078 |
12,874 |
5,631 |
Таблица 2. Показатели эффективности оптимальных торговых моделей.
|
Пара |
15-0,5. |
1-0,5. |
2-1. |
3-2. |
5-3. |
10-5. |
15-10. |
|
Параметры |
SMA5/t0,0015 |
SMA5/t0 |
SMA8/t0 |
SMA13/t0,001 |
SMA13/t0 |
SMA13/t0 |
SMA20/t0,0002 |
|
Коэффициент Шарпа |
-0,214 |
0,539 |
0,669 |
0,764 |
0,202 |
-0,244 |
-0,289 |
|
Месячная волатильность, % |
8,66 |
8,66 |
8,66 |
8,66 |
8,66 |
8,66 |
8,66 |
|
Средняя доходность /месяц, % |
-0,54 |
1,35 |
1,67 |
1,91 |
0,50 |
-0,61 |
-0,72 |
|
Кол-во F |
31 |
43 |
56 |
14 |
37 |
35 |
39 |
|
Кол-во S |
34 |
45 |
29 |
32 |
43 |
45 |
29 |
|
Кол-во 0 |
23 |
0 |
0 |
34 |
0 |
0 |
5 |
|
Кол-во + |
31 |
50 |
49 |
27 |
40 |
41 |
32 |
|
Кол-во - |
34 |
38 |
36 |
19 |
40 |
39 |
36 |
|
Средний выигрыш, % |
6,08 |
6,16 |
6,38 |
10,20 |
6,11 |
4,87 |
6,01 |
|
Средний проигрыш, % |
6,93 |
4,99 |
4,73 |
6,44 |
5,10 |
6,36 |
6,81 |
|
Средний выигрыш /проигрыш |
0,877 |
1,235 |
1,348 |
1,585 |
1,198 |
0,764 |
0,883 |
|
Асимметрия |
-2,529 |
1,28 |
1,908 |
1,825 |
-2,241 |
-2,047 |
-1,132 |
|
Эксцесс |
14,71 |
7,231 |
8,719 |
7,243 |
14,323 |
12,218 |
5,945 |
Положительная асимметрия доходностей наблюдается у оптимальных моделей пар облигаций 1лет-0,5лет, 2лет-1лет и 3лет-2лет, что является положительной характеристикой для торговой модели. По этим парам также имеет место относительно более высокий коэффициент Шарпа. В связи с этим мы делаем вывод, что наибольшую эффективность дает арбитражная торговля инструментами с разницей в сроке погашения не более 1 года.
Количество F и S в таблице означает количество сделок флэтенер (позиция на уменьшение спреда доходности) и стипенер (позиция на увеличение спреда доходности) соответственно, а 0 означает месяцы без сделок. Количество “+” и “-” означает количество прибыльных и убыточных месяцев соответственно. Торговая модель с самым высоким коэффициентом Шарпа (3-2) имеет параметры SMA с периодом 13 и уровень триггера 0,001 (будем называть её моделью SMA13t0,001 – см. таблицу 2.4). Данная торговая модель имеет более чем в два раза превышение прибыльных месяцев над убыточными и превышение в 1,5 раза сделок S над F.
Таблица 3
|
Торговая модель SMA13t0,001 |
||||
|
Тип сделки |
Триггер |
Действие |
Объем |
Срок |
|
Стипенер |
Спотовый спред+0,001<спредSMA13 |
Покупка 2-лет |
3/2=1.5 |
1 месяц |
|
Продажа 3-лет |
1 |
1 месяц |
||
|
Флэтенер |
Спотовый спред>спредSMA13+0,001 |
Продажа 2-лет
|
3/2=1.5 |
1 месяц |
|
Покупка 3-лет |
1 |
1 месяц |
||
Составлено автором
Рисунок 1 отражает арбитражные возможности торговой модели возврата к среднему. Торговая модель SMA13t0,001 показала лучший результат в том числе потому, что спотовый сред доходности пары облигаций 3-летней и 2-летней характеризуется высокой скоростью возврата к среднему, что видно на рисунке 1.
Рисунок 1
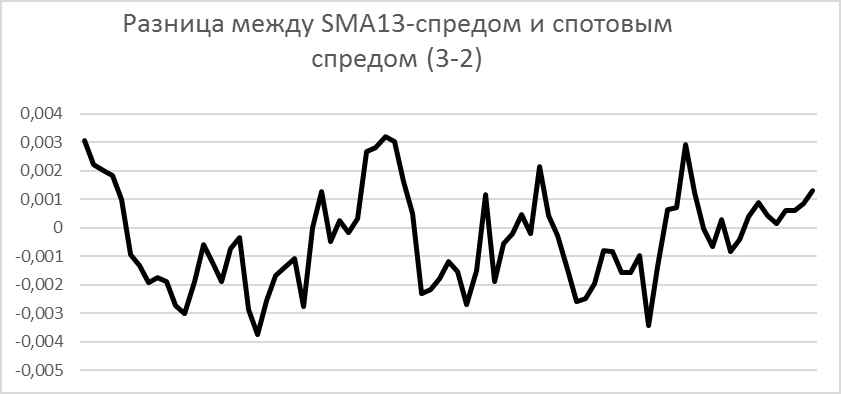
Составлено автором
На рисунке 2 отражена кумулятивная доходность модели SMA13t0,001. Следует учесть, что доходность рассчитана без учета возможных потерь на bid-ask спредах используемых инструментов.
Рисунок 2
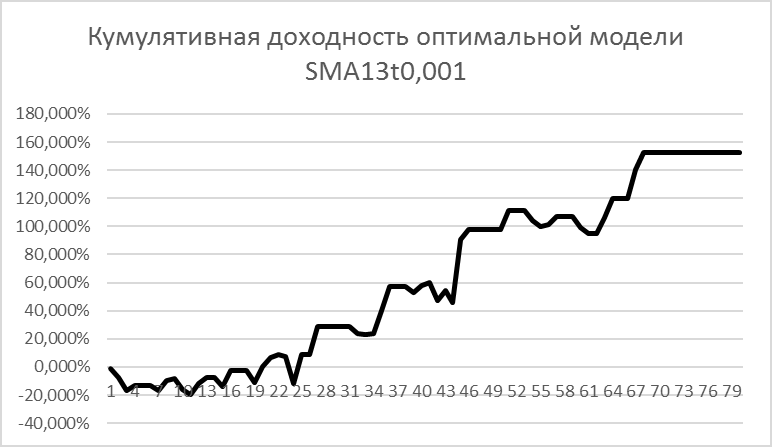
Составлено автором
На рисунке 3 отражена кумулятивная доходность кумулятивной модели пары облигаций 3лет-2лет. Визуальный анализ говорит о более высокой эффективности оптимальной модели, что и подтвердилось более высокими коэффициентом Шарпа и показателем средний выигрыш/проигрыш. Кумулятивная модель также подвержена более глубокой и продолжительной просадке, что говорит о ее большем риске.
Рисунок 3
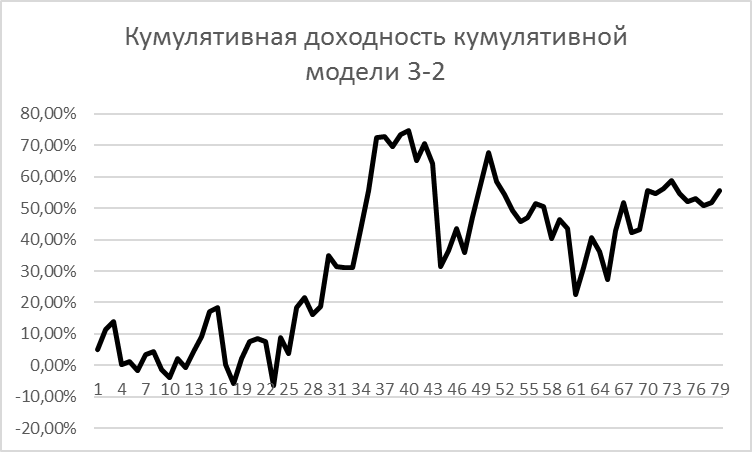
Составлено автором
Сравнение спотового спреда доходности со скользящим средним периода за несколько месяцев (от 5 до 13) для выявления арбитражных возможностей и установка минимальной величины отклонения от среднего, служащего триггером для открытия позиций, позволяет усовершенствовать торговую модель, так как она начинает в таком случае приносить большую доходность без увеличения волатильности, как было показано при тестировании на исторических данных.
Литература
- Shiller R. Campbell J. Schoenholtz K. Forward rates and future policy: interpreting the Term structure of interest rates. // Brookings Papers on Economic Activity, 1983, pp. 173–217. [Электронный ресурс] - Режим доступа: https://www.brookings.edu/wp-content/uploads/1983/01/1983a_bpea_shiller_campbell_schoenholtz_weiss.pdf (дата обращения: 02.08.2018)
- Seo, B. Nonlinear mean reversion in the term structure of interest rates // Journal of Economic Dynamics and Control. V. 27. №11–12. 2003. p. 2243-2265
- Chua C.T. Koh T.H. Ramaswamy K. Profiting from Mean-Reverting Yield Curve Trading Strategies // Journal of Fixed Income. 2006. V 15. № 4. p. 20-33.
- Duarte J. Longstaff F. A. Yu F. Risk and Return in Fixed-Income Arbitrage: Nickels in Front of a Steamroller? // The Review of Financial Studies. 2007. №3. p. 769-811.
- A. Rambaldini / How to Interpolate Interest Rates [Электронный ресурс] – Режим доступа: https://www.sapling.com/8396129/interpolate-interest-rates (дата обращения: 20.04.2018)
- Sharpe W. The Sharpe Ratio // Journal of Portfolio Management. 1994. V. 21. №1. p. 49-58.
- Martellini L. Priaulet P. Priaulet S. Understanding the butterfly strategy // Research and innovation notes. 2002. № 1. p. 1-14.
- Fabozzi F. J. Mann S.V. Handbook of fixed-income securities / New York: McGraw-Hill, 2012. 1809 p.
- Sangwon Suh S., Kimb Y. J. Covered interest parity and arbitrage paradox in emerging markets: Evidence from the Korean market // Pacific-Basin Finance Journal. 2016 V. 38. June. p. 161-176
- Wong A. High R. Fixed-income arbitrage: analytical techniques and strategies / New York: Willey Finance Edition. 1993. 254 p.